- Простейшие картинки
- Мишка-жонглёр
- Блюдо с фруктами
- Предложения для 3-летних творцов
- Ёлочка
- Курица с выводком
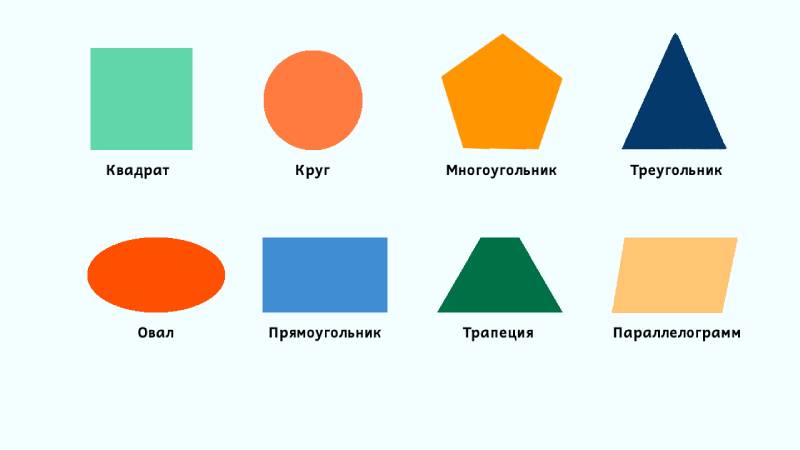
- Карточки с геометрическими фигурами для детей
- Основные понятия
- Счет геометрических фигур
- Создание аппликаций из геометрических фигурок
- Где встречаются геометрические фигуры в нашей жизни?
- Особенности работы с геометрическими фигурами в разном возрасте
- Плоские геометрические фигуры из бумаги – Строим замок
- Объемные геометрические фигуры из бумаги – Вырезаем и клеим:
- Простая модель из бумаги для детей
- Изучаем простых бумажных животных: как сделать фигурки своими руками
- Параллелограмм и ромб
- Основные величины и их формулы
- Периметр
- Площадь
- Вычисление периметра и площади
- Композиция фотографии
- Сюжетный центр фотографии
- Равновесие снимка
- Перспектива
- Играть в лото
- Польза геометрической аппликации для развития дошкольников
- Фигура куб: описание
- Для учеников 1 класса
- Фигура тетраэдр: описание
Простейшие картинки
Детки 1-2 годиков только знакомятся с окружающим миром
Их важно обучить наклеиванию, исключая чёткую композицию. Занятие проводится в виде игры
Мишка-жонглёр
Следует придумать историю, как медведь потерял мячики для жонглирования. Целью выступает знакомство малышей с кругом, закрепление знаний об оттенках, формирование навыков обращения с клеящим веществом. Потребуется:
- кружки разного размера и цветные листы;
- медвежий образ, как яркая наклейка;
- картон;
- клей, в составе которого крахмал или мука;
- сухая и влажная салфетка.
Рассказывая случай, как весёлый медвежонок растерял мячики, наклейте персонаж. Помогите ребёнку отыскать эти шары, отличающиеся объёмом и тоном. Теперь маленькому мастеру предстоит самому, смазывая детали от центральной части к краю, расположить их вокруг Топтыгина и, используя сухую тряпочку, прижать к основанию.
Блюдо с фруктами
Это более сложная поделка, закрепляющая полученные знания. Рисуется и вырезается тарелка или корзинка. В неё детки осуществляют доставку изображений яблок, груш, винограда, сопоставляя их по геометрическим конфигурациям. После этого повторяются названия вкусных предметов и цветовая гамма. Тут же можно попробовать сделать гусеницу, которая не против того, чтобы полакомиться ими.
Предложения для 3-летних творцов
В этом возрасте ребятишки смогут помещать на смысловом фоне несколько элементов. Изделия выглядят представителями флоры и фауны, хорошо знакомыми им. Когда творение готово, не забудьте похвалить создателя и вставить полотно в фото рамку на память.
Ёлочка
Займитесь изготовлением красивой поздравительной открытки к Новому году. Для этого потребуются:
- Три зелёных треугольника.
- Любые мелкие детали различной формы.
- Гелиевые блёстки.
Сложив бумажный лист надвое, на сгибе располагают ёлку, восходящую ввысь, начиная от большого элемента к малому
Обращайте внимание, чтобы была соблюдена вертикальная линия. Из остальных мелочей мастерят гирлянды, флажки, между которыми красуются новогодние шарики
По кайме произведения создают блестящий узор.
Курица с выводком
Взрослые готовят нужный вариант, нарисовав курочку. Малыши дополняют образец, оформляя силуэты цыплят, дорисовывая глаза-точки, клювики. Не лишне предложить внести добавочные украшения – солнышко, травка в облике прямоугольных полосок, цветочки – треугольники.
Карточки с геометрическими фигурами для детей
Изучать геометрические фигуры можно с помощью карточек с их изображением. С этим материалом можно придумать разные игры для детей до 6 лет. Запомнить геометрические фигуры помогут следующие игры с карточками:
- Взрослый поочерёдно называет геометрические фигуры, а ребёнок ищет их изображения на карточках.
- Поиск парных изображений фигур среди перевернутых карточек.
- Счёт одинаковых фигур в ряде.
- Дополнение последовательности карточек изображением недостающей фигуры.
- Классификация по признаку формы.
Достоинство этого обучающего материала в том, что карточки всегда можно взять с собой и позаниматься изучением и повторением геометрических фигур где угодно. Их можно купить, а можно изготовить самостоятельно, скачав подходящие картинки с геометрическими фигурами из интернета.
Знакомство ребёнка с основами геометрии в раннем возрасте помогает малышу всецело познавать окружающий мир и успешно освоить точные науки в школе. Начинать стоит с творческих занятий и с упражнений в игровой форме. Старайтесь вплетать названия геометрических фигур и форм в ваш ежедневный диалог с ребёнком, но не переборщите с этим. Поддерживайте интерес к изучению геометрии с помощью подходящих сортеров, конструкторов, мозаик и других игровых наборов.
Основные понятия
Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.
Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Примеры объемных геометрических фигур:
- шар,
- конус,
- параллелепипед,
- цилиндр,
- пирамида,
- сфера.
Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Пройти урок
Счет геометрических фигур
Дидактическая игра на закрепление знаний количественого и порядкового счета с помощью использования геометрических фигур.
План дидактической игры на закрепление порядкового счета с геометрическими фигурами:
- На листе нарисовано пять квадратов. Покажи третий квадрат.
- На листе нарисовано шесть треугольников. Покажи второй треугольник.
- На листе нарисовано семь кругов. Покажи второй круг.
План дидактической игры на закрепление количественного счета с геометрическими фигурами:
- Выложи перед собой три круга и два квадрата. Сколько всего фигур расположено перед тобой?
- Выложи два круга и один треугольник. Сколько всего фигур расположено перед тобой?
- Выложи один ромб и 5 трапеций. Сколько всего фигур получилось?
Для закрепления знаний на тему «геометрические телах и фигуры» стоит проводить повторные занятия 1 раз в неделю.
Геометрические фигуры для детей развивающее задание:
- Расположи геометрические фигуры на листе бумаги по размеру в порядке возрастания.
- Расположи геометрические фигуры на листе бумаги по размеру в порядке убывания.
Создание аппликаций из геометрических фигурок
Для начала ребёнка надо познакомить с геометрией, показав и объяснив различие предметов по форме, чтобы, работая, он самостоятельно подбирал детали. Перед началом процесса, подготовьте рабочую область:
- Освободите стол, покрыв его защитной плёнкой.
- Предварительно заготовьте нужные элементы.
- Пользуйтесь безопасными ножницами, имеющими тупые концы.
- Приготовьте картонку или иную плотную основу.
- Обзаведитесь клеем, цветной бумагой насыщенных тонов.
Малыша надо ознакомить с последовательностью действий и техникой приклеивания заготовок. Проводить работу желательно совместно.
Где встречаются геометрические фигуры в нашей жизни?
Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах.
Люди давно заинтересовались разнообразием геометрических фигур. Ещё для первобытных людей важную роль играла форма окружавших их предметов. Овладевая миром, люди знакомились с простейшими геометрическими формами. Сначала они изготавливали орудия труда относительно правильной формы, потом научились их совершенствовать. Специальных названий для геометрических фигур тогда, конечно, не было. Их придумали значительно позже. Когда люди стали строить дома, им пришлось ещё глубже разбираться в особенностях разных фигур, чтобы понять, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна или каменные глыбы. Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.
И в современном мире без этих знаний не прожить.
Где же встречаются геометрические фигуры в нашей жизни?
Возможно, кто-то считает, что различные линии фигуры «водятся» только в книгах учёных математиков. Однако, если посмотреть вокруг, становится понятно, что многие предметы имеют форму, похожую на основные геометрические фигуры. Просто мы не всегда это замечаем. Немало замечательных геометрических фигур встречается в окружающей нас природе. Поле имеет форму прямоугольника, река — кривой линии, озеро — круга, кристалл соли — форму куба, обычная горошинка, капелька росы — форму шара. Красивы и разнообразны многогранники — кристаллы горного хрусталя. Но и в привычной жизни основные геометрические фигуры тоже повсюду. Это здания, строения, транспорт, интерьер квартиры, даже посуда и предметы одежды. К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр.
Знать все фигуры, их виды, названия и свойства очень важно. Систематизирует знания о геометрических фигурах и изучает их свойства математическая наука — геометрия
Наука эта очень важная, её применение просто бесценно во все времена и независимо от профессии. Без знаний геометрии не обходится ни рабочий, ни инженер, ни архитектор, ни художник. И очень важно начать осваивать эту науку в раннем возрасте.
Прекрасным помощником ребёнку в этом станет образовательная платформа iSmart. Основные виды геометрических фигур, их свойства, задачи на нахождение площади фигур и многое другое есть на платформе в разделе «Математика». Тут собраны несколько тысяч заданий на освоение этих тем, не повторяющиеся при многократной отработке. Занимаясь на , школьники начальных классов досконально разберутся в основах геометрии. Это даст им хорошую базу по предмету для учёбы в средних и старших классах. Кроме того, интерактивные задания красочные, интересные, увлекательные.
Итак,
Особенности работы с геометрическими фигурами в разном возрасте
Поделки из фигур доступны для занятий с детьми с самого младшего возраста.
Для малышей 2-4 лет задание не должно включать в себя больше 5 деталей
В противном случае ребенок быстро устает, путается, а внимание его рассеивается. Для изготовления поделки малышу необходимо приготовить готовые элементы поделки из цветной бумаги и предложить основу с готовым контуром
Или показать, последовательность выполнения работы. Дети в возрасте 4-5 лет могут вырезать из бумаги простые детали самостоятельно, но под присмотром взрослых. Для работы ребенку необходимы ножницы с закругленными концами. Дети такого возраста способны сами выполнить поделки средней сложности. Учащиеся младших классов справляются самостоятельно с достаточно сложными заданиями.
Для того, чтобы заинтересовать ребенка изготовлением поделки из геометрических фигур, можно предложить ему интерактивную игру на основе сказки “Мышонок и карандаш”. Затею эту можно осуществить в домашних условиях на занятиях в детском саду. Необходимо заранее приготовить элементы, из которых состоит кошка: круги, овалы и треугольники.
Увлекательная игра поможет сделать творческий процесс интереснее для очень активных детей.
Плоские геометрические фигуры из бумаги – Строим замок
В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).
После этого подробно объесните ребенку инструкцию к выполнению упражнения.
“Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными. Вот например, один из них”, – взрослый показывает одну или две игровых схемы замка с нашего задания. – “Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.” – взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.
Карточка 1
Карточка 2
Карточка 3
Карточка 4
Карточка 5
Карточка 6
Геометрические фигуры для вырезания:
Объемные геометрические фигуры из бумаги – Вырезаем и клеим:
- Итак, в первом листе мы выложили следующие геометрические фигуры: куб (фигура, поверхность которого состоит из 6 квадратов), трехгранная пирамида (основание пирамиды и 3 грани), четырехгранная пирамида (основание и 4 грани), ромб (фигура, визуально состоящая из двух пирамид, имеющих общее основание).
- Во втором листе вы найдете развертки таких геометрических фигур из бумаги: шестигранник (фигура, состоящая из шести граней), цилиндр (состоящий из свернутого прямоугольника и двух окружностей-оснований) и конус.
Лист 1
Лист 2
После того, как дети, при помощи взрослых, склеят все геометрические фигуры из бумаги, можно продолжить занятие, задавая детям вопросы. Например: “Покажи мне пирамиду. Сколько у нее сторон? Где ее основание? Чем эта пирамида (показываете трехгранную) отличается от этой (четырехгранной)? Покажи мне цилиндр. Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?” – и так далее.
В зависимости от возраста ребенка, можно использовать в занятии различные обучающие материалы.
Например, что такое пирамида:
Какие бывают пирамиды. (Пусть ребенок покажет из них те, которые он склеил)
Что такое куб:
Что такое конус и цилиндр. На что они похожи:
Простая модель из бумаги для детей
Для развития у малыша логики и мелкой моторики, специалисты решили создавать фигуры, но с меньшим уровнем сложности. Ребёнок будет доволен, если вы предложите ему сборку забавных фигурок.
Моделирование из бумаги и картона в примерах.
Изучаем простых бумажных животных: как сделать фигурки своими руками
Предлагаем вам научиться делать элементарные и оригинальные фигурки животных из бумажных листов. Для начинающих рукодельниц такие схемы и описания очень простые и доступные в исполнении.
Из простого бумажного листа можно сделать смешную и забавную фигурку собаки. Возьмите лист бумаги квадратной формы и загните его верхние углы. Затем необходимо сложить лист по диагональному направлению широкой стороной наверх. Далее следует загнуть верхние острые концы по направлению вперед и вниз. Это будут уши вашей бумажной собаки. Теперь уголок, который образовался в результате данных мероприятий вам необходимо загнуть назад.
Далее на мордочке животного вам необходимо нарисовать глаза и нос вашей собачки. Для более наглядного и понятного восприятия процесса изготовления бумажного животного можете посмотреть несколько схем, представленных на фото ниже.
Ели же вы завернете уголки, расположенные сверху, не по направлению вперед, а назад, то вы сможете сделать фигурку кота.
Еще проще и быстрее можно сформировать нежные и завораживающие фигурки певчих птичек из бумажного материала. Подберите красивую декоративную бумагу с красочным принтом и нарисуйте или поищите в Интернете желаемый шаблон птички.
Из декоративной бумажной материи контрастного оттенка необходимо вырезать крыло птички, которое затем прикрепить на основу птицы, вырезанную из бумаги. Теперь проденьте декоративный шнур через отверстие красочной пуговицы и завяжите красивым бантиком. Далее приклейте при помощи крепкого клея на заготовку пуговицу с декоративным бантиком.
При помощи дырокола из листа бумаги сделайте кружочки для формирования глаз птички. Осталось приклеить их на правильное место. Ваша бумажная певчая птичка готова.
Для того чтобы выполнить такую простую и оригинальную композицию из бумажного материала, понадобятся лист цветной бумаги красного оттенка и лист бумаги зеленого цвета.
Сначала бумажную заготовку в виде квадрата со сторонами восемь с половиной сантиметров, вырезанную из листа бумаги красного оттенка, необходимо два раза сложить по диагональному направлению. Затем левую сторону и правую сторону квадрата следует согнуть внутрь. Далее вам необходимо обрезать уголки таким образом, чтобы туловище божьей коровки приобрело овальную форму. Для завершения бумажной оригинальной поделки, туловище божьей коровки необходимо разрисовать и приклеить фигурку на лист бумаги зеленого цветового оттенка. Теперь ваша объемная композиция завершена.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны
Ромб — это параллелограмм с равными сторонами.
Свойства параллелограмма:
- Противоположные стороны и углы равны.
- Сумма любых двух соседних углов равна 180 градусам.
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит фигуру на два равных треугольника.
Общие формулы расчета площади фигур:
- S = a × h, где a — сторона, h — высота.
- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. В случае с ромбом стороны равны, поэтому формула примет вид S = a × a × sinα или S = a2 × sinα.
- Для ромба: S = 0,5 × (d1 × d2), где d1,d2 — две диагонали. Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Периметр ромба — это произведение длины стороны на четыре.
P = 4 × a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Основные величины и их формулы
Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.
Периметр
Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:
На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
Обозначается заглавной латинской P.
Площадь
Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь.
На рисунке площади фигур окрашены различными цветами.
Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.
Вычисление периметра и площади
Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.
- Квадрат: периметр = 4 * сторона.
- Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
- Неправильный многоугольник: периметр = сумме всех сторон многоугольника.
- Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).
Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:
- Параллелограмм: площадь = основание * высота
- Квадрат: площадь = сторона 1 * сторона 2
- Треугольник: площадь = ½ * основание * высота
- Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).
Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:
- интерактивные задания больше похожи на игру;
- их можно отрабатывать многократно и они не будут повторяться;
- платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;
- достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.
Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.
Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.
Композиция фотографии
Композиция — это соединение или составление отдельных частей в одно целое. В фотографии существует много приёмов, позволяющих получить гармоничное и впечатляющее изображение. Такие снимки занимают призовые места на различных выставках, по ним изучают искусство композиции начинающие фотографы. Существует несколько следующих правил, соблюдая которые можно получать почти идеальные снимки:
- Наличие сюжетного центра;
- Равновесие снимка;
- Правильный выбор перспективы;
- Удачный задний план.
Кроме того правильно выстроенная композиция кадра не должна быть слишком пустой или, наоборот, перегруженной лишними объектами.
Сюжетный центр фотографии
Смысловой или сюжетный центр фотографии – это тот самый важный объект, ради которого затевалась фотосессия. Слово центр не означает, что предмет съёмки должен находиться в середине снимка, хотя фото для домашнего альбома выполняются именно таким образом. Для получения выразительной фотографии нужно использовать принцип деления кадра на девять частей или «правило третей». Самые важные объекты снимка должны располагаться в точках, где линии пересекаются или, в крайнем случае, на самих линиях. На этих точках, прежде всего, фокусируется взгляд зрителя. Важным в композиции является «правило диагоналей». Фотография, где дорога пересекает снимок от нижнего правого к левому верхнему углу, намного выразительней и динамичней снимка с дорогой, идущей параллельно нижней границе кадра.
Равновесие снимка
Геометрическое равновесие снимка является важной частью композиции. Самым простым способом добиться баланса фотографии это поместить основной объект в середину, но такой снимок лишён выразительности и не вызывает никаких эмоций
Смещение предмета влево или вправо, на точки пересечения линий, будет правильным решением, но это вызовет ощущение «перевешивания» снимка на один край. В этом случае, для того чтобы уравновесить кадр, нужно чем-то заполнить свободное место на фотографии. Уравновешивающий предмет не обязательно должен иметь такие же размеры, что и основной объект. Чем ближе предмет к краю изображения, тем больше его кажущийся «вес». Важную роль играет цветовая составляющая. Красные тона и оттенки кажутся более тяжёлыми, чем голубые и зелёные цвета.
Перспектива
Правильный выбор перспективы позволит на плоской фотографии передать глубину пространства, поэтому удачным решением будет присутствие на композиции нескольких планов, удалённых друг от друга. В таких композициях важную роль играет яркость отдельных зон. Так, если основной объект светлых тонов, задний план должен быть более тёмным, и наоборот
Фон не должен быть перегружен большим количеством второстепенных деталей, так как они будут отвлекать внимание от доминанты снимка. Соблюдать основные правила композиции совсем не сложно
Несколько труднее выделить на снимке различные геометрические фигуры. Они присутствуют на любом снимке и могут определять общее настроение снимка.
Играть в лото
Кому-то может показаться, что для 1,5-годовалого ребенка еще слишком рано играть в лото, но это не так, он вполне может с ним справиться.
В зависимости от того, какое лото вы выберете, оно может быть полезным при изучении названий цветов, животных, фруктов, овощей, транспорта, геометрических фигур и т.п. Ведь во время игры вы будете проговаривать все наименования (Пример цветного лото можно СКАЧАТЬ ЗДЕСЬ).
Самый первый вариант игры, который вы можете попробовать, — это просто вместе с малышом подбирать карточки к игровому полю с картинками. Когда такое занятие немного приестся ребенку, можно попробовать его разнообразить, например, таким образом: кладем игровое поле на стульчик, а карточки – в другую часть комнаты. Затем говорим малышу: «Давай поможем чебурашке собрать лото. Но карточки так далеко! Будем вместе возить их на машине!» И затем начинаем вместе с ребенком и чебурашкой загружать карточки в машину и отвозить их к назначенному месту. Можно не сразу доставать все карточки, а подкладывать их партиями, чтобы малышу пришлось сделать несколько заездов. Скорее всего, ребенку очень понравится такая версия игры.
Малышам чуть постарше (ближе к 2 годам) становится интересно играть с каким-нибудь партнером: к примеру, мама дает одно игровое поле малышу, а второе – мишке или папе, затем, доставая поочередно карточки, начинает спрашивать «у кого есть лошадь? а у кого корова?». Желательно доставать карточки так, чтобы ребенку не приходилось подолгу ждать своей очереди (иначе он заскучает) и в то же время, чтобы он учился быть терпеливым во время хода другого участника. В общем, оптимально, если участники будут получать карточки поочередно:)
Польза геометрической аппликации для развития дошкольников
Начиная с младшего дошкольного возраста и до 1 класса упражнения по соединению простых фигур в единое изображение очень полезны для детей. Самым маленьким они помогают узнать и запомнить, какие бывают геометрические фигуры, закрепить названия цветов.
Занятия этим видом аппликации также развивают:
- мелкую моторику;
- аккуратность;
- глазомер;
- усидчивость и внимательность;
- навыки работы с ножницами и клеем;
- воображение, способность нестандартно мыслить (треугольник похож на мордочку лисы или кусочек сыра);
- способность конструировать, учитывая то, в каком порядке фигуры будут располагаться на готовой поделке — части, которые должны быть дальше, наклеиваются первыми, а те, что ближе к смотрящему, могут наслаиваться на предыдущие (например, если медведь стоит вполоборота, сначала к фону крепится одна его лапа, потом туловище, и только затем вторая лапа).
Кроме того, процесс подбора нужных деталей и их составления закладывает в сознание маленьких творцов понимание того, что многое в окружающем мире состоит из геометрических фигур, а сложное складывается из простого.
Фигура куб: описание
Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и прямоугольной призмой, у которой основание является квадратом, а высота равна стороне основания.
Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В — 2 = 6 + 8 — 2 = 12.
Если обозначить буквой «a» длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a3 и S = 6*a2, соответственно.
Для учеников 1 класса
Дети уже более или менее владеют ножницами, когда идут в 1 класс. Шаблоны в этом случае станут незаменимыми помощниками. С помощью них дети смогут вырезать нужные детали из бумаги, и им будет проще творить и учиться делать аппликации. Вот шаблоны нескольких несложных геометрических аппликаций:
Аппликация «Домик в деревне»:
Вроде бы ничего сложного, никаких сложных деталей. Все просто. Домик, солнышко, дерево, но есть в этой картине что-то необыкновенное. Кроме того, ребенок сделает эту картину еще более уникальной, ведь она будет воплощением его фантазии и мышления.
Аппликация «Кошка с котенком»:
Для изготовления аппликации этой кошечки с котенком ребенку нужно будет вырезать самые разнообразные фигуры и составить из них целостный образ по своему вкусу.
Аппликация «Веселая гусеница»:
Веселая гусеница позабавит ваших детишек. Ее интересно не только рассматривать, но и делать. Ведь эти кружочки и другие детали можно расположить по-разному. И у каждого ребенка получится своя неповторимая веселая гусеница.
Для изготовления вышеперечисленных аппликаций домика, кошки и гусеницы можно просто распечатать схемы, затем дети могут вырезать фигурки и приклеить их на бумагу. Но это уж слишком просто. Так что можно сделать шаблоны своими руками. И тогда дети будут вырезать по ним из разных цветов части и приклеивать их.
Фигура тетраэдр: описание
Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.
Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a3*√2/12 и S = √3*a2, где a — длина стороны равностороннего треугольника.
Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH4, в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.
Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.